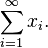աջորդականությունը, մաթեմատիկայում, օբյեկտների (կամ իրադարձությունների)
կարգավորված ցանկ է: Բազմանդամի նման, այն պարունակում է անդամներ
(որոնք նաև կոչվում են էլեմենտներ կամտարրեր), և տարրերի քանակը
(հնարավորինս անսահման) կոչվում է հաջորդականության երկարություն:
Ի տարբերություն բազմանդամի, կարգը
նշանակություն ունի, և ճիշտ նույն էլեմենտները կարող են բազմաթիվ անգամներ
հայտնվել հաջորդականության տարբեր դիրքերում: Հաջորդականությունը դիսկրետ ֆունկցիա է:
Օրինակ, (C, R, Y) տառերի հաջորդականություն է, որը տարբերվում է (Y, C, R)-ից, քանի
որ կարգավորությունը նշանակություն ունի: Հաջորդականությունները կարող են լինել
սահմանափակ, ինչպես այս օրինակում է, կամ անսահմանափակ, ինչպես դրական
զույգ թվերը (2, 4, 6,...), դրական և բացասական ամբողջ թվերը: Սահամանափակ
հաջորդականությունները երբեմն անվանում են տողեր կամ բառեր, իսկ անսահմանափակ
հաջորդականությունները հոսքեր: Դատարկ
հաջորդականությունը() ներառված է հաջորդականության հասկացությունների մեծ մասի մեջ,
բայց կարող է բացառվել կախված համատեքստից:
Մաթեմատիկայում կան հաջորդականությունների` բազմազան և միանգամայն տարբեր
Օրինակ և նշագրություն
հասկացություններ, որոնցից մի քանիսը (օրինակ, ճշմարիտ հաջորդականությունը)կազմված չեն
ստորև ներկայացված նշագրությամբ:
Բացի այդ հաջորդականության էլեմենտների ճանաչումը իրենց դիրքերի միջոցով, ինչպես օրինակ
"3-րդ էլեմենտը", էլեմենտներին կարող են տրվել անուններ, հարմար հղման համար:
Օրինակ հաջորդականությունը կարող է գրվել այսպես` (a1, a2, a2, … ), or (b0, b1,b2, … ), կամ
(c0, c2, c4, … ), կածված նրանից` որն է պիտանի հավելվածում:
Սահմանափակ և անսահմանափակ
Սահմանափակ հաջորդականության ավելի պաշտոնական սահմանումը S
բազմության տարրերի միջոցով ֆունկցիա է {1, 2, ..., n}-ից մինչև S շատ մեծ n > 0 համար:
Անսահմանափակ հաջորդականությունը S-ում ֆունկցիա է {1, 2, ... }-ից մինչև S:
Օրինակ, պարզ թվերի հաջորդականությունը (2,3,5,7,11, … )
հետևյալ ֆունկցիան է 1→2, 2→3, 3→5, 4→7, 5→11, … :
Հաջորդականության սահմանափակ երկարությունը`
n կոչվում է նաև ''n''-կորտեժ:
Սահամանափակ հաջորդականությունները ներառում են
դատարկ հաջորդականություն ( ),
որը չունի էլեմենտներ:
Հավաքածուում բոլոր ամբողջ թվերից ֆունկցիան երբեմն կոչվում է bi-անսահմանափակ
հաջորդականություն կամ երկկողմանի անսահմանափակ հաջորդականություն:
Օրինակը բոլոր զույգ ամբողջ թվերի bi-անսահմանափակ հաջորդականությունն է
( … , -4, -2, 0, 2, 4, 6, 8… ):
Մուլտիպլիկատիվ
Դիցուք` A = (հաջորդականություն սահմանափակված f ֆունկցիայով:
{1, 2, 3, ...} → {1, 2, 3, ...}, այնպես որ a i = f(i):
Հաջորդականությունը մուլտիպլիկատիվ է եթե f(xy) = f(x)f(y) բոլոր x,y համար, ա
յնպես որ x և y
փոխադարձաբար պարզ են:
Հաջորդականությունների տեսակները և հատկությունները
Տրված հաջորդականության ենթահաջորդականությունը հաջորդականություն է,
որը կազմված է` որոշ էլեմենտներ ջնջելով, առանց խախտելու մնացած էլեմենտների
հարաբերական դիրքերը:
Եթե հաջորդականության տարրերը կարգավորված բազմության ենթաբազմություն է,
ապա մոնոտոն աճող հաջորդականությունը մի հաջորդականություն է, որի յուրաքանչյուր
տարր ավելի մեծ է, քան իրեն նախորդողը կամ հավասար է նախորդողին: Եթե յուրաքանչյուր
տարր խիստ ավելի մեծ է, քան նախորդը, հաջորդականությունը կոչվում է մոնոտոն խիստ աճող:
ոնոտոն նվազող հաջորդականությունը սահմանվում է նմանապես. Ցանկացած հաջորդականություն,
որը բավարարում է մոնոտոնության հատկությանը կոչվում է մոնոտոնային կամ
մոնոտոն:Սա մոնոտոն ֆունկցիայի ավելի ընդհանուր հասկացության հատուկ դեպքն է:
Չնվազող և չաճող տերմինները օգտագործվում են ցանկացած հնարավոր շփոթմունքներից
խուսափելու համար` կապված խիստ աճելու և խիստ նվազելու հետ:
Եթե հաջորդականության տարրերը ամբողջ թվեր են, ապա հաջորդականությունը
ամբողջ հաջորդականություն է: Եթե հաջորդականության տարրերը բազմանդամներ են,
ապա հաջորդականությունը բազմանդամ հաջորդականություն է:
Եթե S-ը օժտված է տոպոլոգիայով, ապա հնարավոր է դառնում որոշել անսահմանափակ
հաջորդականության զուգամիտությունը S-ում: Այսպիսի որոշումները ներառում են
հաջորդականության սահման հասկացությունը:
Եթե A-ն բազմանդամ է, ազատ մոնոիդը A-ի նկատմամբ (նշանակված է A*) մոնոիդ
պարունակում է
բոլոր սահմանափակ հաջորդականությունները (կամ տողերը)կազմված զրո կամ ավելի
A-ի էլեմենտներից,
զուգամիտության երկուական գործողությամբ:Ազատ կիսախումբը A+, A*-ի կիսախումբ
է, որը պարունակում է
բոլոր էլեմենտները, բացի դատարկ հաջորդականությունից:
Հաջորդականությունների վերլուծությունը
Վերլուծություններում, երբ խոսվում է հաջորդականությունների մասին, ընդհանրապես
նկատի է առնվում հետևյալ տեսքի հաջորդականությունը

ըստ որի, էլեմենտների անսահմանափակ հաջորդականությունը ինդեքսավորված է բնական թվերով:
Հարմար կլինի ունենալ հաջորդականություն, որ սկսվում է 1-ից կամ 0-ից տարբեր ինդեքսով:
Օրինակ, հաջորդականությունը կազմվածxn = 1/log(n)-ով որոշված կլինի միայն n ≥ 2 համար:
Երբ խոսվում է այսպիսի անսահմանափակ հաջորդականությունների մասին, սովորաբար բավական է
(և շատ բան չի փոխի նկատառումների մեծամասնության համար)ենթադրել, որ հաջորդականության
անդամները սահմանված են նվազագույնը բոլոր բավական մեծ ցուցանիշների համար, որը ավելի մեծ
է քան ինչ-որ տրված N:
Հաջորդականությունների ամենապարզ տեսակը թվայինն է, որոնք իրական կամ կոմպլեքս թվերի
հաջորդականություն է: Այս տեսակը կարող է ընդհանրացվել ինչ-որ վեկտորական տարածության
էլեմենտների հաջորդականության: Վերլուծություններում, վեկտորական տարածությունները հաճախ
ֆունկցիոնալ տարածություններ են: Ավելի ընդհանուր, հաջորդականությունները կարելի է
ուսումնասիրել ինչ-որ տոպոլոգիական տարածության էլեմենտներով:
Շարքեր
Հաջորդականության էլեմենտների գումարը շարք է:Ավելի ճիշտ, եթե (x1, x2, x3, ...)
հաջորդականություն է, կարելի է որոշել մասնակի գումարների հաջորդականությունը` (S1, S2, S3, ...)
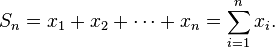 միջոցով:
միջոցով:
Ձևականորեն, այս հաջորդականությունների զույգը ներառում է շարքեր x1, x2, x3, ...էլեմենտներով,
որը նշանակվում է այսպես
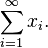
Եթե մասնակի գումարների հաջորդականությունը զուգամետ է, ապա նրա սահմանի համար նաև
օգտագործվում է անսահմանափակ գումարի նշագրությունը: Ավելի մանրամասն, նայիր շարքեր:
Անսահմանափակ հաջորդականությունները տեսական
համակարգչային գիտությունում
Թվային սիմվոլների (կամ բնութագրեր)ահսահմանափակ հաջորդականությունները
կազմված սահմանափակ այբուբենից հատուկ հետաքրքրություն են ներկայացնում
տեսական համակարգչային գիտությունում: Դրանք հաճախ հղվում են
որպեսհաջորդականություններ կամ հոսքեր, որպես սահմանափակ տողերին հակադիր:
Անսահմանափակ երկուական հաջորդականությունները, օրինակ, բիթերի
(բնութագրեր կազմված {0,1} այբուբենից) անսահմանափակ հաջորդականություններ են:
Բոլոր անսահմանափակ, երկուական հաջորդականությունների C = {0, 1}∞
բազմությունը երբեմն կոչվում է Քենթորի տարածություն:
Անսահմանափակ երկուական հաջորդականությունները կարող են ներկայացնել
պաշտոնական լեզու (տողերի բազմություն)` նշանակելով հաջորդականության n րդ բիթը 1,
միայն և միայն այն դեպքում, եթե n րդ տողը(շորթլեքս կարգում) կա լեզվում:Ուստի,կոմպլեքս
տեսակների ուսումնասիրությունը, որոնք լեզուների բազմություն են, կարող են դիտարկվել
որպես անսահմանափակ հաջորդականությունների բազմության ուսումնասիրություն:
Անսահմանափակ հաջորդականությունը կազմված {0, 1, ..., b−1} այբուբենից կարող է նաև
ներկայացնել իրական թիվ` արտահայտվածb-հիմքով դիրքային թվային համակարգում:
Այս համարժեքությունը հաճախ օգտագործվում է իրական վերլուծության տեխնիկան
կոմպլեքսային տեսակների բերելու նպատակով:
Հաջորդականություններ և ավտոմատներ
Ավտոմատները կամ սահմանափակ հաղորդման մեքենաները կարող են
ենթադրվել որպեսուղղորդված դիագրամներ, նշված առավելություններով
օգտագործելով հատուկ այբուբեն Σ: Մի հաղորդումից մյուսին ավտոմատ անցնելու
ամենատարածված տեսակները մուտքագրված սիմվոլների կարդալն է Σ-ից;
կարգավորված մուտքը այսպիսի ավտոմոտների համար հաջորդականությունն
անվանում է բառ (կամ մուտքային բառ):Հաղորդումների հաջորդականությունը,
որոնք հանդիպում են ավտոմատի կողմից բառի մշակման շամանակ, կոչվում է հոսք:
Չդետերմինացված ավտոմոտը կարող է ունենալ չնշված կամ կրկնօրինակ ելք ամեն
հաղորդման համար, որը տալիս է ավելին քան մեկ հաղորդողը ինչ-որ մուտքի սիմվոլի:
ՍԱ ուղղակի ենտադրում է մի քանի հնարավոր հոսքերի ստեղծում տրված բառի համար,
յուրաքանչյուրը լինելով մեկ հաղորդման հաջորդականություն, այլ ոչ թե մեկ հաղորդման
ստեղծում, որը հաղորդումների բազմությ
ան հաջորդականություն է; այնուամենայնիվ, 'հոսք'ը երբեմն օգտագործվում է նշանակելով
վերջում ասվածը:

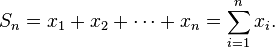 միջոցով:
միջոցով: