Զուգահեռագիծ է կոչվում այն քառանկյունը, որի հանդիպակաց կողմերը
զույգ առ զույգզուգահեռ են, այսինքն, հանդիպակաց կողմերը
գտնվում են զուգահեռ ուղիղների վրա: Զուգահեռագծի մասնավոր
օրինակներ են ուղղանկյունը,քառակուսին և շեղանկյունը:
 - Զուգահեռագիծ
|
Զուգահեռագծի հիմնական հատկությունները
- Զուգահեռագծի հանդիպակաց կողմերը հավասար են:
 .
.
Ապացույց: AB || CD => < ABD = < BDC, հետևում է խաչադիր անկյունների
հավասարությունից AD || BC => < ADB = < DBC, DB-ն ընդհանուր է ուրեմն
ABD և BCD եռանկյունները հավասար են: Դրանից հետևում է, որ AD - ն
հավասար է BC - ին և AB -ն հավասար է BC -ին:
- Զուգահեռագծի հանդիպակաց անկյունները հավասար են:
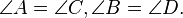
- Զուգահեռագծի անկյունագծերը հատվում են և հատման կետում կիսվում են:
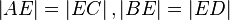 .
.
Ապացույց՝ BC = AD ըստ առաջին հատկության, <ADE = < EBC, < ECB = < EAD
(խաչադիր անկյուններ) => եռանկյուններ AED -ն և BEC - ն հավասար են, ուրեմն
AE = EC, DE = EB:
- Զուգահեռագծի կողմին առընթեր անկյունների գումարը 180° է :
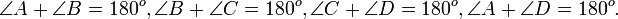
- Զուգահեռագծի ցանկացած անկյունագիծ այն բաժանում է 2 հավասար եռանկյունների:
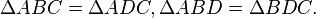
- Զուգահեռագծի անկյունագծերի հատման կետը հանդիսանում է զուգահեռագիծի
- սիմետրիայի կենտրոնը:
- Զուգահեռագծի անկյունների գումարը հավասար է 360°:
- Զուգահեռագծի անկյունագծերի քառակուսիների գումարը հավասար է
- բոլոր կողմերի քառակուսիների գումարին:
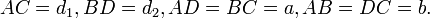
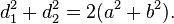
Զուգահեռագծի հայտանիշները
ABCD քառանկյունը զուգահեռագիծ է, եթե կատարվում է հետևյալ պայմաններից որևէ մեկը՝
- Հանդիպակաց կողմերը զույգ առ զույգ հավասար են.
 .
.
- Հանդիպակաց անկյունները զույգ առ զույգ հավասար են.
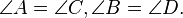
- Անկյունագծերը հատման կետում կիսվում են.
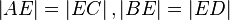 .
.
- Կողմին առընթեր անկյունների գումարը 180° է.
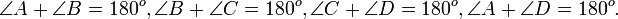
- Հանդիպակաց կողմերը իրար զուգահեռ են և հավասար.
 .
.
Ապացույց: < EAD = < ECB, < EDA = < EBC => Եռանկյուն AED -ն հավասար է եռակյուն
BEC => AE = EC, BE = DE, < AEB = < CED (< AED = < BEC, հակադիր անկյունների
հավասարությունից, իսկ <AED -ն և <BEA -ն կից են) => եռանկյուն AEB = եռանկյուն DEC:
Դրանից հետևում է, որ AB -ն զուգահեռ է DC -ին: Ուրեմն ABCD -ն զուգահեռագիծ է:
- Ուռուցիկ քառանկյան հանդիպակաց կողմերի միջնակետերի միջև
- հեռավորությունների գումարը հավասար է նրա կիսապարագծին.
- Զուգահեռագծի անկյունագծերի քառակուսիների գումարը հավասար
- է կողմերի քառակուսիների կրկնապատիկների գումարին.
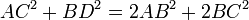
Զուգահեռագծի մակերեսը
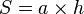 , որտեղ
, որտեղ  -ն կողմն է,
-ն կողմն է, 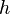 -ը`այդ կողմին տարված բարձրությունը:
-ը`այդ կողմին տարված բարձրությունը: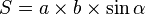 , որտեղ
, որտեղ  -ն և
-ն և 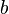 -ն կողմերն են, իսկ
-ն կողմերն են, իսկ 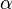 - ն
- ն  և
և 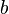 կողմերի
կողմերի - կազմած անկյունն է:
 :
:
Զուգահեռագծի պարագիծը
 , որտեղ
, որտեղ  -ն և
-ն և 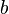 -ն զուգահեռագծի կողմերն են:
-ն զուգահեռագծի կողմերն են:

 .
.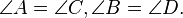
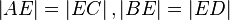 .
.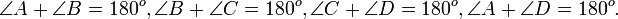
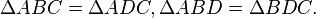
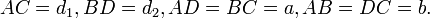
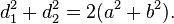
 .
.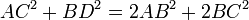
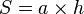 , որտեղ
, որտեղ  -ն կողմն է,
-ն կողմն է, 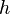 -ը`այդ կողմին տարված բարձրությունը:
-ը`այդ կողմին տարված բարձրությունը: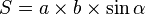 , որտեղ
, որտեղ 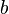 -ն կողմերն են, իսկ
-ն կողմերն են, իսկ 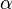 - ն
- ն  :
: , որտեղ
, որտեղ